
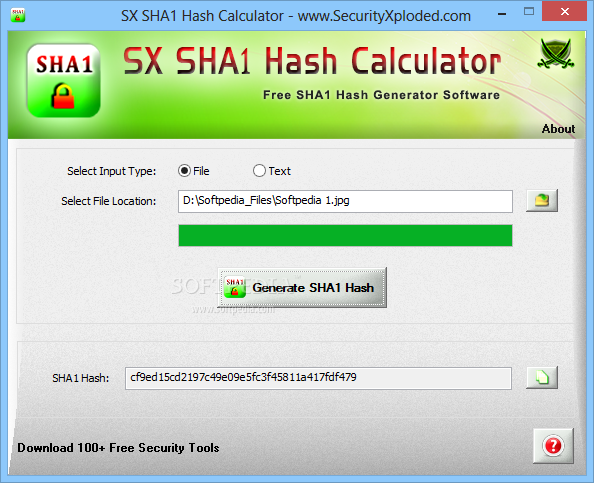
Some years ago you would protect your passwords from hackers by storing SHA256 encrypted password in the your data base. So it is no longer recommended to use it for password protection or other similar use cases. With the newest hardware (CPU and GPU) improvements it is become possible to decrypt SHA256 algorithm back. This makes it suitable for checking integrity of your data, challenge hash authentication, anti-tamper, digital signatures, blockchain.
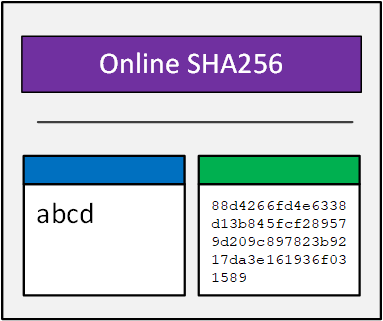
SHA256 algorithm generates an almost-unique, fixed size 256-bit (32-byte) hash. Even if only one symbol is changed the algorithm will produce different hash value. If you would like to compare two sets of raw data (source of the file, text or similar) it is always better to hash it and compare SHA256 values. A cryptographic hash is like a signature for a data set. In every round we will be calculating another 6 variables - S 1, ch, t 1, S 0, maj and t 2.The SHA (Secure Hash Algorithm) is one of a number of cryptographic hash functions. We initialize them with our hash variables h 0- h 7. Now, when we finally made all preparations, calculated all the constants, words and initial hashes, we can start.ĭuring calculations we will be messing with 8 variables - A, B, C, D, E, F, G, H. If it is not completely clear how s 0 and s 1 were calculated, you can look at it closer: ← Chunk 0 → ← w 0, 0 → Directly from message ↓ + + + = ↓ Here you can see how every word is calculated: ⋙ means right rotation (circular shift of bits when bits are removed from the end of the word and prepended to the beginning), ≫ means right shift (last bits are removed, zeros are prepended). Here s 0(w) and s 1(w) are calculated as follows: To generate the rest 48 words we use a combination of previous words: If we split our chunk to 32-bit words, we will get 16 words. As we want to do 64 rounds, we need to generate 64 32-bit words from our chunk. Our chunk contains 512 bits and in every round we will work with 32-bit numbers. These rounds look a bit messy, but it is what you want to make the output as random as possible. For the first round of the first chunk we use initial hash values from Step 2. For every round we use one of the round constants k that we generated earlier. For each chunk we make 64 rounds of bitwise operations to change hash values h.We split our message to 512 bits chunks.What we are going to do is the following:
k are taken from cubic roots of first 64 prime numbers, i.e. h are taken from square roots of first 8 prime numbers, i.e. We will need 8 initial hash values h and 64 round constants k. They come from fractional parts of square and cubic roots of prime numbers. In SHA-256 initial hash values and round constants are much more transparent. So people were thinking, what if NSA included some kind of backdoor in these constants to be able to get some information about the message just by looking at the hash? In SHA-1 algorithm all initial values were chosen by NSA, who developed that algorithm (yes, for real). So it makes sense to add some randomness from the very beginning. Output of any hashing function should look as random as possible. Now, when we have the message of correct length, we can finally start hashing. Here gray bytes represent padding (additional bits to make the message length multiple of 64) and red bytes shows encoded length of the message in bits. Right after the message we add one bit equal to 1 and then put zeros to make total length in bits multiple of 512. The length should be appended at the very end of the message. We need to append to the message its length in bits as a 64-bit integer and make the total length at least 512 bits long (64 bytes) or multiple of it. Visual SHA-256 calculator Enter your message here: Resulting hashĬurrently our message is 480 bits long ( 60 bytes).


 0 kommentar(er)
0 kommentar(er)
